siliconcros.blogg.se

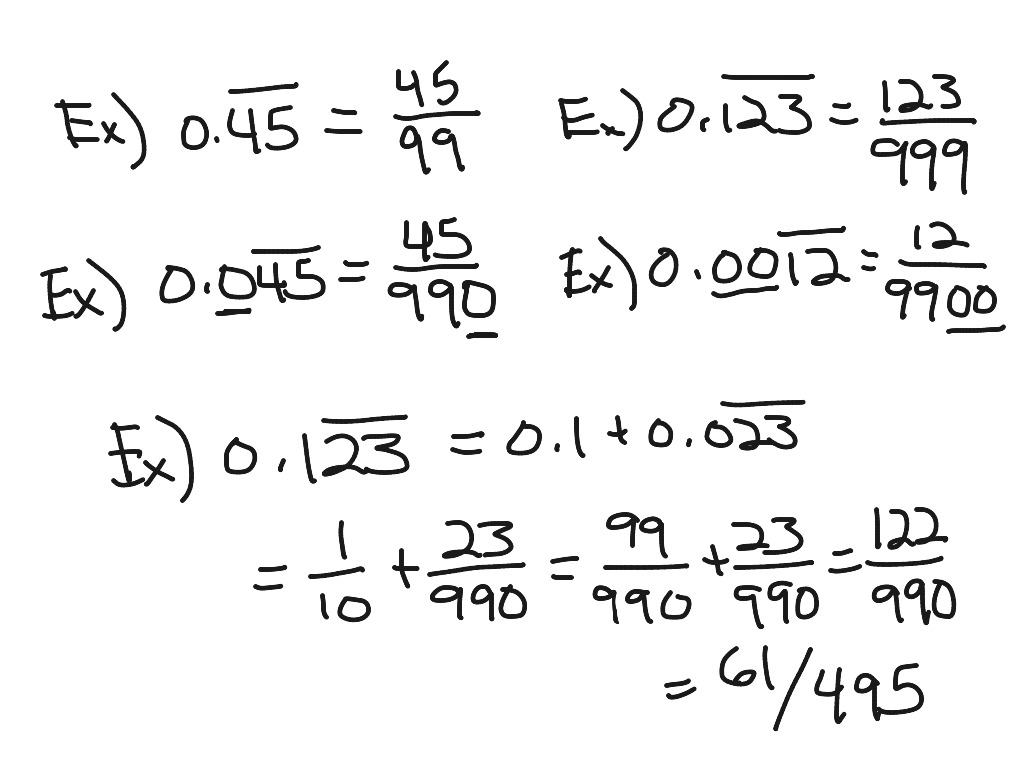
1. Converting recurring decimals to fractions how to#
2. Converting recurring decimals to fractions series#

" So once again, they start to ask themselves some very interesting philosophical questions.

The robot society celebrates the fact that they have reached the number of 100 robots too, and this is a very important moment for this robot society, as they begin to realize that they're growing, and at the same time, they have a limit, as they're not supposed to be able to create new robots or being more robots than 100, and if they cannot create that new technology with the mentality that the robots of this society have, what do they have? And moreover, as they grow both in quantity and in knowledge, they start to worry that they might make the same mistakes as humans." Everything starts in this sequel 100 years after the events of the first title, as I've said. " And this sequel is not going to be different, of course. So robots became the successors of humans, and this raises different philosophical questions such as, can we consider that robots are living beings? Can they really supplant humanity and its cognitive and creative capacities? These are, broadly speaking, the main questions raised in the first title."

Converting recurring decimals to fractions series#

" And well, in case that you haven't played the first game or don't know what the theme of the series is, basically the main story is based around the fact that humanity disappeared because of a virus that they accidentally let out. And well, just for you to know, Talos Principle 2 is a thought-provoking first-person puzzle experience that greatly expands on the first game's philosophical themes and stunning environments." Today we're going to talk about Talos Principle 2, one of the games that I checked out at Gamescom, of course, Gamescom 2023.

Converting recurring decimals to fractions how to#

I still don't know how to call them, and I think I'm going to start every video just like this." on the right side, we are subtracting away the same value." Hello everyone, and welcome to a brand new Gamereactor Gamescom Impressions video. So when we subtract away x on the left side and subtract away 0.888. Since x is equal to 0.888., this means they are the same value. Now we will subtract the original equation away from the new equation:īefore we go any further, think about why this is legal? We know the addition property of equality allows us to add or subtract the same value to or from both sides of the equation. We will multiply both sides of our equation by 10: This means n is 1 and 10 to the power of 1 is just 10.

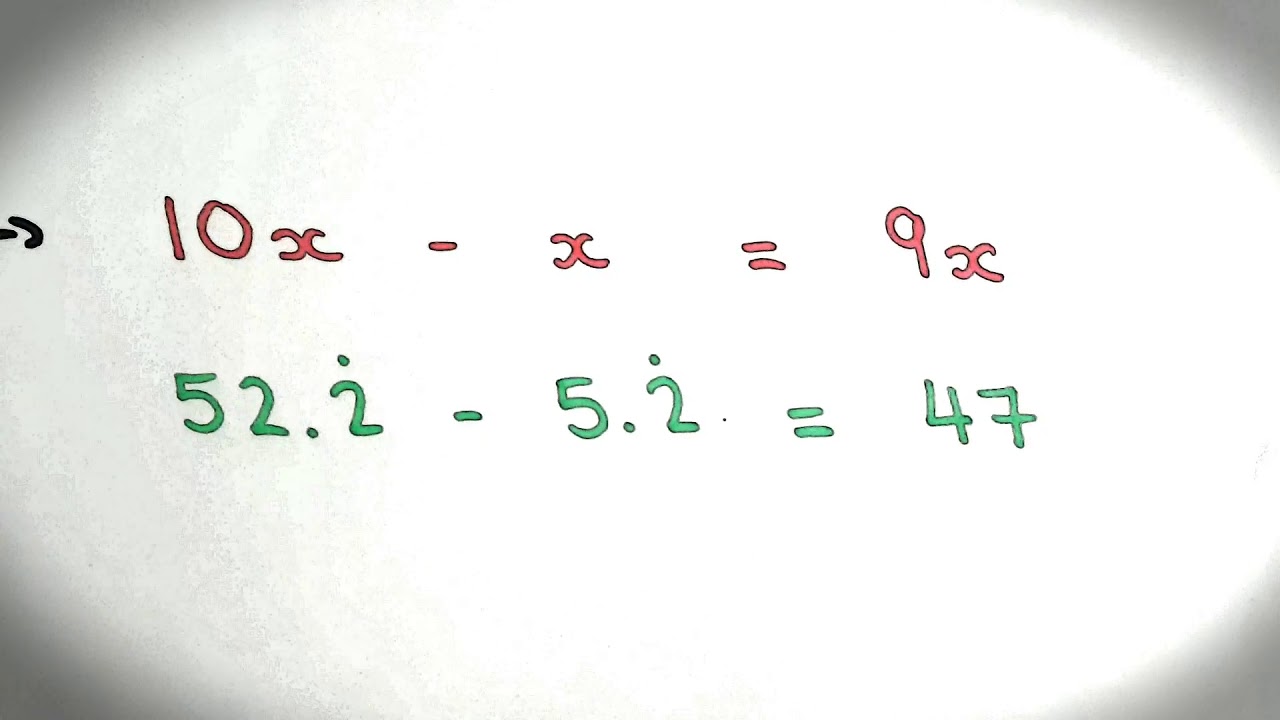
In our case, we have one digit 8, that repeats forever. Next, we will multiply both sides of the equation by 10 n, where n is the number of digits in the repeating pattern. It is normally easier to think about this problem using the ellipsis format. Let's begin by setting our repeating decimal equal to a variable like x:

To convert a repeating decimal to a fraction, we rely on our knowledge of the addition property of equality, along with the multiplication property of equality. When we use the ellipsis, we must ensure that the digit that repeats or pattern of repeating digits is crystal clear. We may also see an ellipsis used instead of an overbar: 9138 » The pattern "9138" repeats forever Let's take a look at a few examples.Ģ.5 32 » The pattern "32" repeats foreverĠ. We generally place a bar over the digit or pattern of digits that repeat. A repeating decimal is a decimal number that repeats the same ending digit or pattern of ending digits forever. Up to this point, we have not discussed how to convert a repeating decimal into a fraction. In our pre-algebra course, we learned how to convert from a decimal to a fraction and from a fraction to a decimal.